Largeur participante des poutres en T — guide complet
Comprendre la largeur participante (ou largeur effective) est indispensable pour dimensionner correctement une poutre en T formée par une nervure et sa dalle. Ci-dessous, nous reprenons le contenu technique de référence, en l’expliquant simplement, pas à pas, avec formules et conseils pratico-pratiques.
1) Qu’appelle-t-on « largeur participante » ?
Dans une poutre intégrée à un plancher, la table de compression est située dans la dalle. Mais toute la dalle ne travaille pas avec la nervure : seule une portion raisonnable est considérée participante. Cette portion est la beff, la largeur participante.
Pourquoi la limiter ? Pour rester réaliste et sécuritaire. Les contraintes ne se diffusent pas à l’infini dans la dalle : au-delà d’une certaine distance, la contribution supplémentaire devient marginale ou non uniforme.
2) Hypothèses usuelles & longueur de référence ℓ₀
On raisonne entre deux points de moment nul. La distance qui les sépare est la ℓ₀. Dans les cas courants :
- Près d’un appui de poutre continue : ℓ₀ = 0,85·ℓ₁
- Au centre d’une travée courante : ℓ₀ = 0,7·ℓ₂
- À la jonction de deux travées : ℓ₀ = 0,15·(ℓ₁ + ℓ₂)
- Console : on retient ℓ₃ = ℓ₂/2
Et pour deux travées consécutives on s’assure de la proportionnalité : ⅔·ℓ₁ ≤ ℓ₂ ≤ 3/2·ℓ₁.
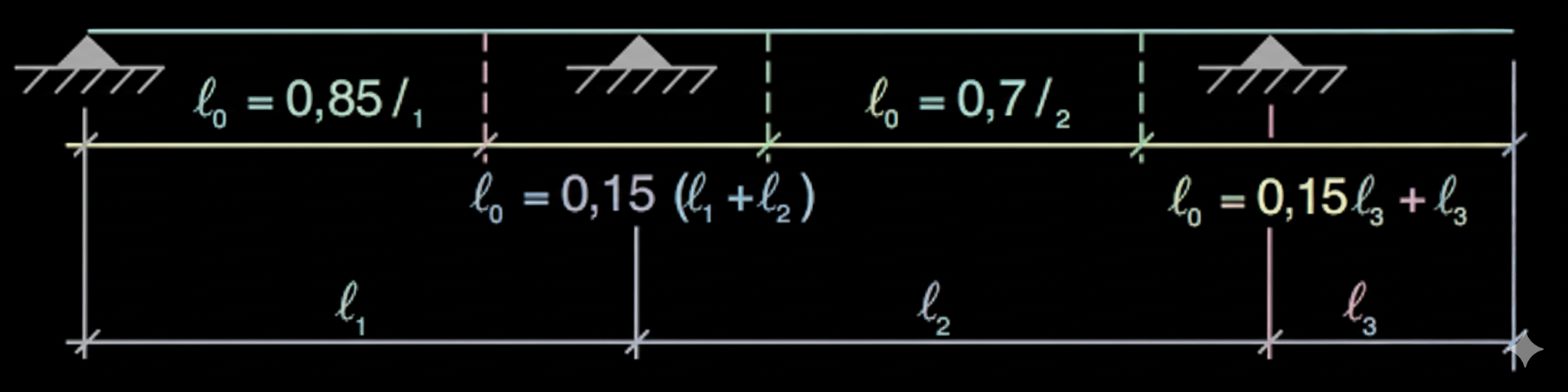
3) Principe de calcul de beff
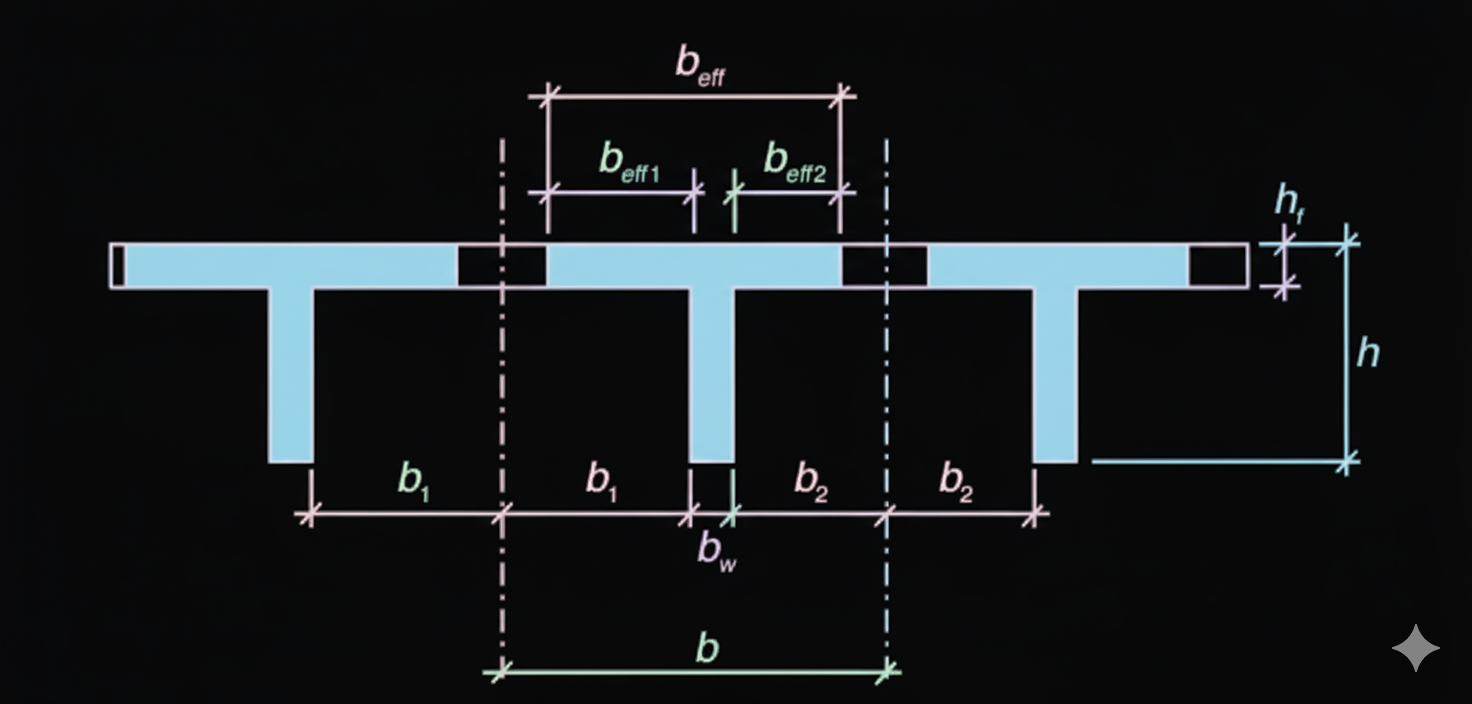
La largeur participante totale comprend la nervure (bw) et les contributions latérales de part et d’autre : beff,1, beff,2, etc. On additionne ces contributions mais on plafonne le tout à une valeur raisonnable pour ne pas sur-évaluer la section comprimée.
beff = Min ( Σ beff,i + bw , b )
où b est la largeur géométrique totale disponible (par exemple, largeur entre axes de nervures adjacentes).
Règle locale côté i
beff,i = Min ( 0,2·bi + 0,10·ℓ₀ ; 0,2·ℓ₀ ; bi )
Interprétation conviviale :
- 0,2·bi + 0,10·ℓ₀ ajoute un terme « géométrie locale + diffusion » ;
- 0,2·ℓ₀ limite l’étendue pour éviter un effet trop optimiste ;
- bi reste évidemment une borne supérieure : on ne dépasse pas la disponibilité réelle.
4) Lecture rapide du schéma de la table comprimée
5) Procédure de calcul pas à pas
- Identifier la configuration (poutre continue, jonction de travées, console…).
- Évaluer ℓ₀ selon la règle adaptée (cf. §2).
- Mesurer les disponibilités latérales : bi de chaque côté de la nervure (jusqu’à l’axe de la nervure voisine, une rive libre, un joint, etc.).
- Calculer chaque contribution beff,i avec la formule locale (Min des trois expressions).
- Assembler : beff = Min(Σ beff,i + bw, b).
- Vérifier la cohérence (bilan géométrique, positions des joints, éventuels évidements, ouvertures de réservation, etc.).
- Utiliser beff pour le calcul de la section en T (position de la fibre neutre, moment résistant, contraintes écrasement…).
6) Exemple numérique guidé (simplifié)
Considérons une travée courante de longueur ℓ₂ = 6,0 m, avec nervures espacées de b = 0,60 m, une nervure de bw = 0,20 m et des disponibilités latérales b1=0,20 m et b2=0,20 m (d’une rive à l’axe voisin).
- Longueur de référence : ℓ₀ = 0,7·ℓ₂ = 0,7×6,0 = 4,20 m.
- Contributions latérales (côté 1 et 2 identiques) :
0,2·bi + 0,10·ℓ₀ = 0,2×0,20 + 0,10×4,20 = 0,04 + 0,42 = 0,46 m
0,2·ℓ₀ = 0,84 m ; bi = 0,20 m
D’où beff,i = Min(0,46 ; 0,84 ; 0,20) = 0,20 m. - Largeur totale : Σ beff,i + bw = 0,20 + 0,20 + 0,20 = 0,60 m, et Min(0,60; b=0,60) = 0,60 m.
Résultat : beff = 0,60 m. Ici, la largeur participante atteint la largeur géométrique disponible — cas fréquent lorsque l’entraxe est modéré et la travée suffisamment longue.
7) Bonnes pratiques & pièges courants
- Uniformité des contraintes : la définition suppose une répartition raisonnablement uniforme dans la bande comprimée. Si ce n’est pas le cas (trous, variations d’épaisseur), réduisez beff ou vérifiez par modélisation.
- Transitions de rigidité : chape rapportée, rupteurs thermiques, bandes de coffrage — autant d’éléments qui peuvent casser l’hypothèse d’un travail « plein » de la dalle.
- Entreâxe variable : si l’entraxe des nervures varie, privilégiez la valeur défavorable localement.
- Voisinage d’une rive libre : la disponibilité bi peut être limitée par la distance à la rive — attention aux façades en encorbellement.
- Console : n’oubliez pas la règle dédiée (cf. ℓ₃ = ℓ₂/2) et les ancrages spécifiques des aciers tendus.
8) Simplifications usuelles « chantier »
Lorsque la grande précision n’est pas exigée (planchers continus de bâtiments courants), on peut retenir une largeur participante constante sur toute la portée. Cette pratique, admise dans de nombreux cas, accélère la conception sans compromettre la sécurité — à condition de rester du côté conservatif et d’expliciter l’hypothèse dans les notes de calcul.
9) FAQ express
Quelle différence entre b et beff ?
b est la largeur géométrique disponible (souvent l’entraxe entre nervures). beff est la partie « utile » de cette largeur, plafonnée par les règles de diffusion des contraintes.
Pourquoi la formule comporte-t-elle 0,10·ℓ₀ ?
Ce terme représente, de manière simplifiée, la diffusion des contraintes depuis la nervure. Plus ℓ₀ est grand, plus la table « peut » contribuer, mais elle reste limitée par 0,2·ℓ₀ et par la disponibilité géométrique bi.
Doit-on vérifier les états limites de service (ELS) avec beff ?
Oui : fissuration, flèche et compression béton doivent être cohérents avec la section en T retenue. beff influence la position de la fibre neutre et la rigidité fléchissante.



